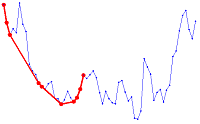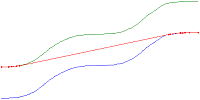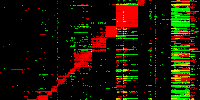
Google Maps based. First visualization of the correlation matrix is based on the Google Maps engine. It is written in Javascript and works on almost any platform.
Silverlight based. Another visualization of the correlation matrix is based on an existing silverlight application, DH view SL, originally developed for viewing large, stitched panoramic images.